Page 5 - 第4部応用事例編ver60_Neat

H１７年度社員教育資料 ・共振周波数 ｆｒ
2端子間のインピーダンスが最小になるときの周波数(共振周波数 fr)は、Z0の式が最小になれば良
水晶発振回路-１ い。そのためには、Z0の式で分子がゼロになる場合であるので、

・X’tal Z min = ω L1 − 1 = 0 これより ω 2 L1C1 = 1 fr = 1
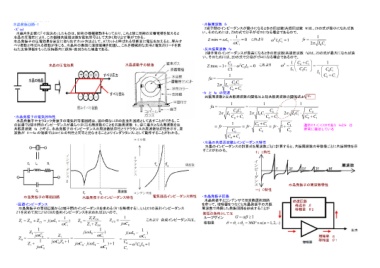
水晶片を正確に「寸法決め」したものは、固有の機械振動をもっており、これと同じ周期の交番電荷を加えると ωC1 2π L1C1
水晶の圧電性により、この機械共振周波数を電気信号として大きく取り出す事ができる。
水晶発振子の圧電効果を安定に取り出すカット方法として、ATカットと呼ばれる切断面に電圧を加えると、厚みす ・反共振周波数 ｆa
べり振動と呼ばれる振動が生じる。水晶片の表面に薄膜電極を配置し、これを機械的な支持と電気的リードを兼
ねた支持薄板をもった保持器内に保持・密封された構造である。

2端子間のインピーダンスが最高になるときの周波数(共振周波数 fa)は、Z0の式が最大になれば良

い。そのためには、Z0の式で分母がゼロになる場合であるので、

水晶の圧電効果 水晶振動子の構造 Z max = 1+ C0 − ω 2C0L1 = 0 これより ω2 = 1 ⎛ C0 + C1 ⎞ = 1
C1 L1 ⎜ C0C1 ⎟
⎝ ⎠ ⎛ C0C1 ⎞
L1 ⎜ C0 + C1 ⎟
fa = 1 ⎠
⎝

2π L1 C0C1
C0 + C1
・fr と ｆa の関連
共振周波数と反共振周波数の関係は上記共振周波数の関係式より=fr

fa = 1= 1= 1
2π
・水晶発振子の電気的特性 L1 C0C1 2π L1C1 C0 2π L1C1 ⋅ C0
水晶発振子やセラミック発振子の電気的等価回路は、図の様なLCRの直並列回路として表すことができる。こ C0 + C1 C0 + C1 C0 + C1
の回路で2端子間のインピーダンスが最も小さくなる周波数のことを共振周波数 fr、逆に最大となる周波数を反
共振周波数 fa と呼ぶ。水晶発振子のインピーダンスの周波数依存性とリアクタンスの周波数依存性を示す。周 = fr ⋅ 1 = fr ⋅ C0 + C1 = fr ⋅ 1+ C1 通常C１＜＜C0であり faとfr は
波数が fr～fa の領域ではコイルの特性と同等と見なせることよりインダクタンスLとして動作することがわかる。 C0 C0 C0 非常に接近している

C0 + C1

・水晶の共振周波数とインピーダンス特性

水晶のインピーダンスの計算式を周波数ごとに計算すると、共振周波数の奇数倍ごとに共振特性を示

すことがわかる。 ＋ｊ L特性

ーｊ C特性 水晶発振子の周波数特性

水晶発振子の等価回路 水晶発振子のインピーダンス特性 電気部品インピーダンス特性 ・水晶発振子回路 帰還回路
帰還率 β
水晶発振子とコンデンサで周波数選択回路 移相量 θ2

・回路インピーダンス を作って、増幅器をつなぐと水晶発振子の共振 増幅率 α
水晶発振子の等価回路から2端子間のインピーダンスを求める（R１を無視する）。L1とC1の直列インピーダンス 移相量 θ1
Z１を求めて次にZ1とC0の並列インピーダンスを求めればよいので、 周波数で持続した発振回路を形成することが

出発来振るの条件としては G = αβ ≥ 1

Z1 = ZL1 + ZC1 = j(ω L1 − 1 ) Z0 = Z1ZC 0 ZC0 = 1 これより 合成インピーダンスは、 ループゲイン
ωC1 Z1 + ZC0 jωC0
移相量 θ = θ1 +θ2 = 360°× n(n = 1, 2,⋅⋅)

Z1 1 Z1 = j(ω L1 − 1 ) j(ω L1 − 1 )
jωC0 jωC0Z1 +1 ωC1 ωC1
Z0 = = =
1 1 C0
Z1 + jωC0 jωC0 ⋅ j (ω L1 − ωC1 ) +1 C1 − ω 2C0 L1 +1