Page 18 - 第4部応用事例編ver60_Neat
P. 18
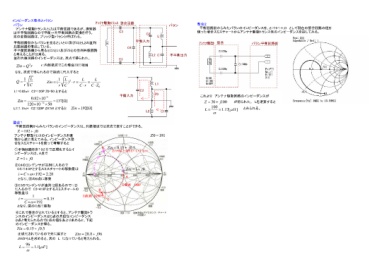
インピーダンス整合とバラン アンテナ駆動トランス 整合回路 バラン 整合2
バラン 不平衡出力 平衡回路側からみたバランのインピーダンスを、Z=191+j0 として現在の整合回路の値を
使った場合スミスチャートからアンテナ駆動トランス側のインピーダンスを探してみる。
アンテナ駆動トランス出力は平衡回路であるが、測定器 C3 C2 L1
は不平衡回路なので平衡→不平衡回路の変換を行う。
図の変換回路は、ブリッジ型バランと呼ばれる。
平衡回路側からバランを見るとL1とC1及びC2とL2の直列 平衡入力 アンテナ駆動 整合 バラン平衡回路側
共振回路を構成している。 C4
不平衡回路側から見るとC2とL1及びZ0との並列共振回路
と考えることが出来る。 L2 C1
並列共振回路のインピーダンスは、次式で得られた。 C3
Zin = Q2r r:内部抵抗でこの場合Z0に相当
Qは、次式で得られるので前式に代入すると
Q=1 L Zin = (1 L )2 ⋅ r = L = L L1
rC rC C ⋅r C ⋅ Z0 Z0
L1=0.82uH C2=120P Z0=50 とすると C2
0.82 ×10−6 平衡入力 これより アンテナ駆動回路のインピーダンスが
120 ×10−12 × 50
Zin = = 137[Ω] Z = 30 + j100 が得られた。 Lを逆算すると
L = 100 = 1.17[μ H ] とみられる。
L1=1.15uH C2=120P Z0=50 とすると Zin = 192[Ω] L2 C1
ω
整合1
平衡回路側からみたバランのインピーダンスは、共振領域では次式で表すことができる。
Z = 192 + j0 Z0 = 191
D Zin = 0.15 + j0.5
アンテナ駆動トランスのインピーダンスを現
物から逆に考えてみる。インピーダンス整 Zin=28.7+j95.5・・L=1.1uH
合をスミスチャートを使って考察すると
①平衡回路側を192Ωで正規化するとイ
ンピーダンスは、A点で
Z =1+ j0
②C4のコンデンサが並列に入るので Zin = 1+ j0
C4=140Pとするスミスチャートの移動量は
A
i = C ×ω ×192 = 2.28
となり、図のB点に移動
③C3のコンデンサが直列(2個あるので1/2) C並列 140P
に入るので C3=410Pとするスミスチャートの B
C直列 820P
移動量は
C
i = 1 = 0.15
C ×ω ×192
となり、図のC点に移動
④これで整合がとれているとすると、アンテナ駆動トラ
ンスのインピーダンスはC点の共役なインピーダンス
D点と考えられるのでD点の値を表より求めると、下記
のインピーダンスを得る。
Zin = 0.15 + j0.5
正規化されているので元に戻すと Zin = 28.8 + j96
J96からLを求めると、次の L になっていると考えられる。
L = 96 = 1.1[μ F ]
ω